Informatica:
Linguaggi e Macchine
Nicola Fanizzi
Dipartimento di Informatica
Università degli Studi di Bari Aldo Moro
Orientamento: 20190225
Cenni Storici..
Inizi 1600 René Descartes (Cartesio)
René Descartes (Cartesio)
- tradurre ogni problema (pratico) in termini matematici
per risolverlo tramite equazioni/calcoli - intuizione applicata al campo geometrico:
- punti come coppie ordinate di numeri
- rette come equazioni di 1° grado in due incognite...

- procedimenti meccanici per il calcolo: Pascalina (addizionatore)

..Cenni Storici..
1666 Leibniz : “Calculemus”
: “Calculemus” propone il ricorso a un calcolo formale per dirimere controversie razionalmente
- Calcolo: per estensione “qualunque notazione che rappresenti il ragionamento, quand'anche non avesse alcun rapporto con i numeri”
- Characteristica Universalis formalizzazione di un linguaggio universale
- Ideazione del Calculus Ratiocinator
- 1671 macchina calcolatrice (Mechanische rekenmachine) capace di simulare la mente umana nelle operazioni aritmetiche


capace (?) di giocare a scacchi
..Cenni Storici..
1837-42 C. Babbage concepì la macchina analitica (analytical engine),
la macchina analitica (analytical engine),primo esempio di macchina universale (hardware),
cui collaborò anche L. Menabrea

e che Ada Lovelace Byron
 corredò del software
corredò del software

..Cenni Storici
1847 G. Boole in The Mathematical Analysis of Logic
in The Mathematical Analysis of Logicpropone l'associazione tra matematica e logica
- logica come scienza delle leggi dei simboli
- prima associata alla filosofia / metafisica
B. riconduce le composizioni degli enunciati a semplici operazioni:
Tempi Moderni
1941 primo calcolatore programmabile moderno Turing-completo:
Z3 di Konrad Zuse

Cronologia dei Linguaggi di Programmazione
Automi
Simboli >> Stringhe >> Linguaggi Formali
Alfabeti
Alfabeto: insieme finito (ma non vuoto) di simboli: $$\Sigma \neq \emptyset$$Esempi
- $\Sigma_{bin} = \{ \mathtt{0,1}\} $
- $\Sigma_{dec} = \{ \mathtt{0,1,2,3,4,5,6,7,8,9} \} $
- $\Sigma_{let} = \{ {\tt a,b,c,d,e,f,g,h,i,j,k,l,}$
$\hspace{3.5em} {\tt m,n,o,p,q,r,s,t,u,v,w,y,z} \}$
Stringhe
Stringa (o parola): sequenza di simboli da un alfabeto $\Sigma$: $$z = s_{[1]} s_{[2]} \cdots s_{[n]}$$ ogni $s_{[i]}$ è un simbolo di $\Sigma$, per ogni posizione $i$- $n$ è la lunghezza della stringa
- $\varepsilon$ indica la stringa senza simboli ($n=0$) detta stringa muta (o parola vuota)
Stringhe | Esempi
- usando $\Sigma_{bin}$: $\varepsilon$, $\mathtt{0}$, $\mathtt{11}$, $\mathtt{101}$, $\mathtt{010101010}$, $\mathtt{101010101}$, ...
- usando $\Sigma_{dec}$: $\varepsilon$, $\mathtt{110}$, $\mathtt{1234567890}$, $\mathtt{33333333}$, ...
- usando $\Sigma_{let}$: $\varepsilon$, $\mathtt{abc}$, $\mathtt{uniba}$, $\mathtt{vercingetorige}$, ...
Chiusura $\Sigma^*$
$$\Sigma^*$$ denota l'insieme (infinito) di tutte le stringhe fatte di simboli scelti da $\Sigma$
Concatenazione (Prodotto)
Operazione "$\cdot$" definita sulle stringhe:date $w_1, w_2$ sullo stesso alfabeto, $$z = w_1 \cdot w_2$$ stringa ottenuta facendo seguire ai simboli di $w_1$ tutti quelli di $w_2$ conservando l'ordine
- op. associativa ma non commutativa
- $\mathtt{20} \cdot \mathtt{19} = \mathtt{2019}$
- $\mathtt{20} \cdot \mathtt{19} \cdot \mathtt{02} \cdot \mathtt{25} = \mathtt{20190225}$
- $\mathtt{automatica} \cdot \mathtt{mente} = \mathtt{automaticamente}$
- $\mathtt{otorino} \cdot \mathtt{laringo} \cdot \mathtt{iatra} = \\ =\mathtt{otorinolaringoiatra}$
- sia $z = w_1 \cdot w_2 \cdot w_3$
- $w_1$ prefisso di $z$
- $w_2$ sottostringa di $z$
- $w_3$ suffisso di $z$
Esempi
Linguaggi Formali
Un linguaggio $L$ su $\Sigma$ è un sotto-insieme di stringhe di $\Sigma^*$: $$L ⊆ \Sigma^∗$$
NB finito, anche vuoto, o infinito
Linguaggi | Esempi
- $\emptyset$ linguaggio vuoto
- $\{ \varepsilon \} = \Sigma^0$ l. composto dalla sola stringa vuota
- $\Sigma = \Sigma^1$ l. delle stringhe di 1 solo simbolo
- $\Sigma^2 = \{s s' \mid s, s' \in \Sigma\}$ l. di tutte le stringhe di lunghezza 2
- $L_2 = (\Sigma_{bin})^2 = \{\mathsf{00,01,10,11}\}$
- $\Sigma^3$ l. delle stringhe di lunghezza 3
... e così via, quindi $\Sigma^* = \displaystyle\bigcup_{n \in \mathbb{N}}\Sigma^n$ - $L' = \{ \mathtt{ababba, aaabbbaaa, aaabbbabaababb} \}$ l. finito
- $L'' = \{\mathtt{a}^n \mathtt{b}^m \mid n,m \in \mathbb{N}\}$ l. infinito
Automi
dal Dizionario
autòma (ant. autòmato) s.m. [dal lat. automătus, gr. αὐτόματος, agg., «che si muove da sé»] (pl. autòmi, ant. autòmati). – 1. Macchina che riproduce i movimenti (e in genere anche l’aspetto esterno) dell’uomo e degli animali. Quindi, fig., persona priva di volontà propria, che agisce o si muove macchinalmente senza coscienza dei proprî atti: camminava come un a.; sembrare, ridursi un automa. 2. In cibernetica (in partic. nella teoria generale degli a.), sistema definito da un insieme di segnali di entrata, di stati interni e di segnali di uscita, e tale che per ogni segnale in entrata fornisce un segnale d’uscita dipendente dallo stato interno in cui il sistema stesso si trova. 3. Nella teoria dei sistemi complessi, a. cellulare, strategia di rappresentazione di sistemi complessi (v. complessità), i cui elementi costituenti sono immaginati come collocati nei nodi di una rete e possono assumere diversi stati a seconda delle interazioni con gli elementi vicini.
Automi Riconoscitori
automa modello astratto di macchina: sistema dinamico discreto e invariante- comportamento indipendente dall'istante in cui agisce
- input su nastro di celle, ciascuna con un simbolo dell'alfabeto d'ingresso $\Sigma$
- convenzione: il nastro scorre verso sinistra, un simbolo alla volta
- l'unità di controllo determina il funzionamento
- in ogni istante, si trova in uno dei suoi stati (memoria interna): $q_0,\ldots, q_n$
- stato iniziale: $q_0$
stati finali: indicano l'accettazione della stringa in input
- stato iniziale: $q_0$
- in ogni istante, si trova in uno dei suoi stati (memoria interna): $q_0,\ldots, q_n$
Automa | Diagramma di transizione
Per descrivere il funzionamento di un automa:
| $\delta$ | $0..9$ | $.$ |
|---|---|---|
| $\to{}A$ | $B$ | |
| $*B$ | $B$ | $C$ |
| $C$ | $D$ | |
| $*D$ | $D$ |
Simulazione di Automi
Grammatiche
Regole >> Derivazioni >> Linguaggi Generati

Grammatica
Una grammatica generativa è un modello astratto
che descrive matematicamente un linguaggio su un dato alfabeto $\Sigma$
-
Si usa anche un altro alfabeto $V$ di variabili o simboli non terminali
- il più importante è il simbolo di partenza, indicato con $S$ (scopo, start)
-
Una regola di riscrittura ha una parte sinistra $\alpha$ e una parte destra $\beta$:
$$\alpha \to \beta$$
$\alpha$ e $\beta$ sono stringhe di simboli da entrambi gli alfabeti $\Sigma \cup V$
Grammatiche - Esempi
| $G_3$: $\Sigma = \{\mathtt{0,1}\}$ e $V = \{S\}$ \[ \begin{eqnarray} S & \to & \mathtt{0} S \\ S & \to & \mathtt{1}\\ \end{eqnarray} \] | $G_2$: $\Sigma = \{\mathtt{0,1}\}$ e $V = \{S,A\}$ \[ \begin{eqnarray} S & \to & \mathtt{0} S \mathtt{0}\\ S & \to & \mathtt{0} A \mathtt{0} \\ A & \to & \mathtt{1}\\ \end{eqnarray} \] |
| $G_1$: $\Sigma = \{\mathtt{a,b,c}\}$ e $V = \{S,A,B\}$ \[ \begin{eqnarray} S & \to & \mathtt{a}BS\mathtt{c}\\ S & \to & \mathtt{abc}\\ B\mathtt{a} & \to & BA\\ BA & \to & \mathtt{a}A\\ \mathtt{a}A & \to & \mathtt{a}B\\ B\mathtt{b} & \to & \mathtt{bb}\\ \end{eqnarray} \] | $G_0$: $\Sigma = \{\mathtt{a,b,c}\}$ e $V = \{S,B\}$ \[ \begin{eqnarray} S & \to & \mathtt{a}BS\mathtt{c}\\ S & \to & \mathtt{abc}\\ B\mathtt{b} & \to & \mathtt{a}B\\ B\mathtt{b} & \to & \mathtt{bb}\\ \end{eqnarray} \] |
Derivazioni
- la derivazione diretta è una relazione tra stringhe, ad es. $\omega, \omega'$, indicata con: $$\omega \Rightarrow \omega'$$
che vale se, data la regola $\alpha \to \beta$,
$\omega' = \gamma \beta \delta$ si ottiene sostituendo $\alpha$ in $\omega = \gamma \alpha \delta$ - La derivazione è la relazione tra stringhe indicata con $$\omega \stackrel{*}{\Rightarrow} \omega'$$ in cui $\omega'$ si ottiene da $\omega$ tramite una sequenza di derivazioni dirette
Derivazioni | Esempi
Data $G_1$ con le regole $\{ S \to \mathtt{0} S \mathtt{1}; S \to \mathtt{10}\}$- derivazione diretta: $\mathtt{000}\underline{S}\mathtt{111} \Rightarrow \mathtt{000}\underline{\mathtt{0}S\mathtt{1}}\mathtt{111}$
- derivazione:
$S \stackrel{*}{\Rightarrow} \mathtt{0000}S\mathtt{1111}$
$S \Rightarrow \mathtt{0}S\mathtt{1} \Rightarrow \mathtt{00}S\mathtt{11} \Rightarrow \mathtt{000}S\mathtt{111} \Rightarrow \mathtt{0000}S\mathtt{1111} $
Linguaggi Generati dalle Grammatiche
Una grammatica $G$ definisce un insieme di stringhe (su $\Sigma$) derivabili da $S$il linguaggio generato da $G$: $$L(G) =\{w \in \Sigma^* \mid S \stackrel{*}{\Rightarrow} w \}$$
Linguaggi Generati da Grammatiche | Esempi
| $G_3$ genera $L(G_3) = \{ \mathtt{0}^i\mathtt{1} \mid i \geq 0 \}$ \[ \begin{eqnarray} S & \to & \mathtt{0} S \\ S & \to & \mathtt{1}\\ \end{eqnarray} \] | $G_2$ genera $L(G_2) = \{ \mathtt{0}^i\mathtt{1}\mathtt{0}^i \mid i > 0 \}$ \[ \begin{eqnarray} S & \to & \mathtt{0} S \mathtt{0}\\ S & \to & \mathtt{0} A \mathtt{0} \\ A & \to & \mathtt{1}\\ \end{eqnarray} \] |
| $G_1$ genera $L(G_1) = \{ \mathtt{a}^i\mathtt{b}^i\mathtt{c}^i \mid i > 0 \}$ \[ \begin{eqnarray} S & \to & \mathtt{a}BS\mathtt{c}\\ S & \to & \mathtt{abc}\\ B\mathtt{a} & \to & BA\\ BA & \to & \mathtt{a}A\\ \mathtt{a}A & \to & \mathtt{a}B\\ B\mathtt{b} & \to & \mathtt{bb}\\ \end{eqnarray} \] | $G_0$ genera $L(G_0) = \{ \mathtt{a}^i\mathtt{b}^i\mathtt{c}^i \mid i > 0 \}$ \[ \begin{eqnarray} S & \to & \mathtt{a}BS\mathtt{c}\\ S & \to & \mathtt{abc}\\ \mathtt{b}A & \to & A\mathtt{b}\\ B\mathtt{b} & \to & \mathtt{bb}\\ \end{eqnarray} \] |
Esempio | derivazione con $G_2$
albero di derivazione
derivazione
Simulatore
Simulatore di Grammatiche Libere @ Stanford
Macchine di Turing
Funzioni e Algoritmi >> Problemi >> Calcolabilità
Richiami | Terminologia..
Funzione relazione che associa elementi di due insiemi $$f: \mathrm{Dominio} \to \mathrm{Codominio}$$ ogni $x \in \mathrm{Dominio}$ è associata ad al più un $y \in \mathrm{Codominio}$- Esempi
- $\cos: \mathbb{R} \to \mathbb{R}$
- $\cdot: \mathbb{S}^2 \to \mathbb{S}$
- $\mathrm{pwd}: \mathbb{UID} \to \mathbb{S}$
- $\mathrm{cf}: \mathbb{Persone} \to \mathbb{S}$
..Richiami | Terminologia
Algoritmo descrizione formale della procedura per risolvere il problema
- dato $x \in \mathrm{Dominio}$ [input]
come ottenere $y=f(x) \in \mathrm{Codominio}$ [output] - descrizione in un numero finito di passi:
ogni passo (elementare) richiede un numero finito di risorse- es. una ricetta
Programma algoritmo scritto in un linguaggio interpretabile da una macchina
Problema della Decisione
 Entscheidungsproblem posto da David Hilbert nel 1928
Entscheidungsproblem posto da David Hilbert nel 1928
❝Esiste una procedura automatica in grado di stabilire, per ogni enunciato espresso nel linguaggio formale della logica del primo ordine, se esso è deducibile o meno all'interno del sistema formale?❞

Macchina di Turing
MdT modello di calcolo ideato da Alan M. Turing nel 1936- idea meccanismo astratto che simuli il lavoro dell'impiegato diligente
- una MdT $M$ consta di
- un nastro $T$ infinito con simboli da $\Sigma$
- una testina $H$ di lettura e scrittura
- un insieme di stati interni $Q$
- un'unità di controllo $CU$ capace di spostare $H$ e di leggere/scrivere un simbolo da/su $T$, secondo un programma interno $\delta_M$
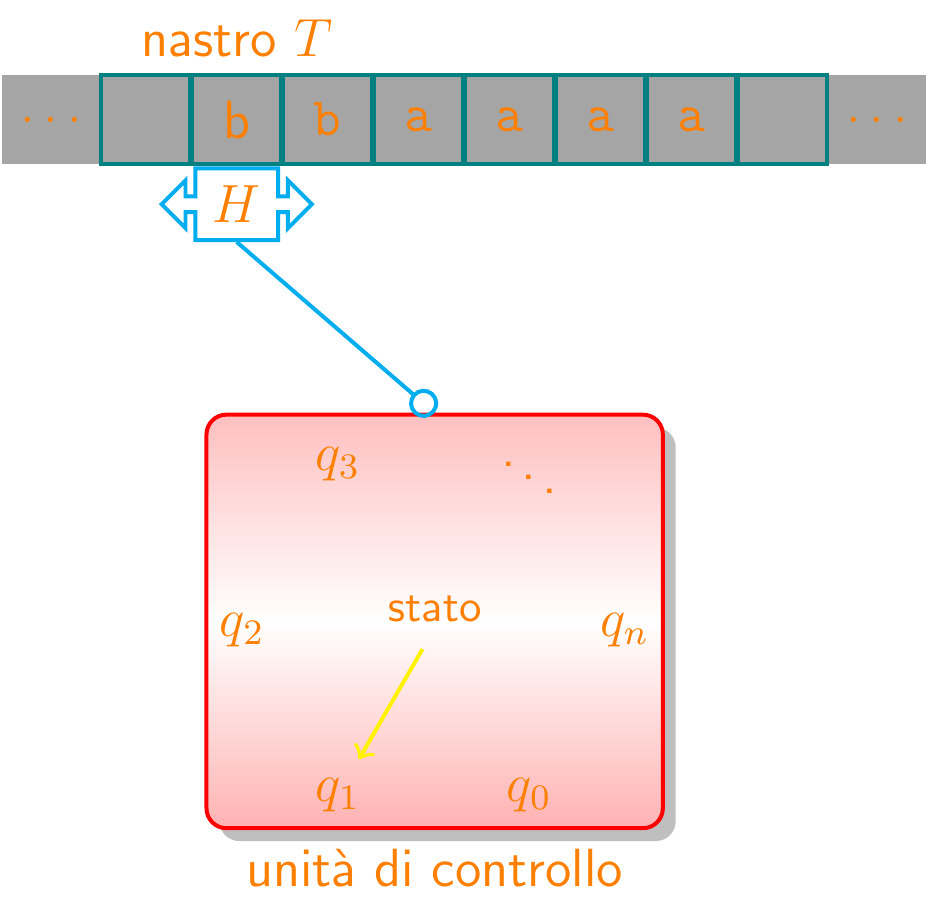
Computazione nella Macchina di Turing

Funzionamento
- a ogni avvio, $M$ si trova nello stato $q_0$
- a ogni passo $CU$,
considerato $q$ corrente e $s$ letto da $H$,
esegue un'istruzione detta transizione: $$\delta_M(q,s) = (q', s', m)$$- passa nello stato $q'$ ($q=q'$ ammissibile)
- scrive $s'$ nella cella di $T$ indicata da $H$
- sposta $H$ di una posizione a sinistra o a destra secondo $m = \pm 1$
Caratteristiche Salienti
- La funzione di transizione $\delta_M$ costituisce un insieme finito di istruzioni
- La MdT è l'agente di calcolo che esegue le istruzioni
- La MdT opera in modo discreto e deterministico
- La MdT può utilizzare il nastro per memorizzare i risultati intermedi
- Nessuna limitazione sulla lunghezza delle stringhe di ingresso:
nastro infinito, una memoria di capacità non limitata
- Nessuna limitazione sulla lunghezza delle stringhe di ingresso:
- Le operazioni che la MdT può eseguire sono semplici, di complessità finita
- Numero delle istruzioni eseguite durante una computazione: illimitato
- Dato che le istruzioni sono di numero finito,
è ammessa la possibilità di eseguire più volte la stessa istruzione - Esiste la possibilità di computazioni infinite
- Dato che le istruzioni sono di numero finito,
MdT, Linguaggi e Problemi
Una mdT decide un linguaggio $L$ su $\Sigma$ se,avendo fissato due stringhe di output che corrispondano a $\text{Sì}$ e $\text{No}$,
essa, ricevendo sul nastro una stringa $w$
- termina rispondendo $\text{Sì}$ quando $w$ appartiene a $L$
- termina rispondendo $\text{No}$ quando $w$ non appartiene a $L$
essa termina la computazione avendo calcolato l'output corretto $f(w)$
- per le altre stringhe può divergere (iterare all'infinito senza terminare)
- funzione parziale
MdT Universale
Risultati Teorici
- Ogni mdT $M$ calcola una funzione $f_M$ definita su stringhe di un dato alfabeto $\Sigma$
- Ogni funzione $f$ calcolabile ha una mdT $M$ che la calcola (Tesi di Turing)
- Ogni mdT $M$ corrisponde a un numero naturale $x$ tramite opportuna codifica
- nel seguito si identificherà la mdT con $M_x$
- Ogni coppia di numeri naturali può essere messo in corrispondenza con un numero naturale (Cantor): $(n,m) \to k$
Algoritmo Universale
Lavorando con numeri naturali $x, y, z$ e con un alfabeto che li rappresenta,consideriamo la funzione così definita: \[ f(x, y, z) = \begin{cases} 1 & \text{$M_x$ converge in $z$ passi sull'input $y$}\\ 0 & \text{altrimenti} \end{cases} \] essa è calcolabile (esiste una mdT che la calcola)
Algoritmo
- eseguire $M_x$ sull'input $y$ per $z$ passi
- se la mdT termina la sua esecuzione entro $z$ passi
- allora termina restituendo in output $1$
- altrimenti (non si è fermata), termina restituendo in output $0$
Macchina Universale
Una MdT $M$ è determinata da $\delta_M$ con le istruzioni per il suo controllo: il suo programma
Teorema Si può costruire una MdT universale $\mathcal{U}$ che simuli il lavoro di ogni altra MdT:
- per ogni $M$, e per ogni input naturale $y$,
$\mathcal{U}$ riceve $(M, y)$ come input e riproduce la computazione di $M$ su $y$ - per avere che l'alfabeto di $\mathcal{U}$ tratti solo numeri:
per ogni MdT $M$ si considera il suo numero di etichetta $x$, ossia $M = M_x$ - $\mathcal{U}$ fornirà come output $M_x$ su $y$, e cioè $M(y)$
Problemi Non Decidibili
Esistono funzioni non calcolabili attraverso una MdTProblema della Terminazione (Halting Problem)
- Si può definire una MdT $\mathcal{H}$ che,
avendo in input un'altra MdT e un suo possibile input $(M,x)$,
sappia decidere se il calcolo di $M(x)$ termini o meno?- ossia $\mathcal{U}$ dovrebbe terminare sempre rispondendo $\mathrm{Sì}$ o $\mathrm{No}$ a seconda della terminazione di $M(x)$ (ossia $M$ applicata al suo input $x$)
Problema della Fermata
La risposta è negativa- Si dimostra per assurdo supponendo che $\mathcal{H}$ esista (quindi anche il suo codice $y_\mathcal{H}$)
- derivando da $\mathcal{H}$ una MdT $\mathcal{D}$ che
- termina quando $\mathcal{H}$ su $y_\mathcal{H}$ non termina
- diverge se $\mathcal{H}$ su $y_\mathcal{H}$ termina
- applicando $\mathcal{D}$ a se stessa (come input):
terminando indicherebbe di non terminare e viceversa (paradosso)
- derivando da $\mathcal{H}$ una MdT $\mathcal{D}$ che
Linguaggi di
Programmazione
Macchine Astratte >> Traduzione >> Gerarchia
Dai Problemi ai Programmi
Problema >> procedura di Soluzione (algoritmo) >> Programma
descrizione informale $\longleftarrow \longrightarrow $ descrizione formale
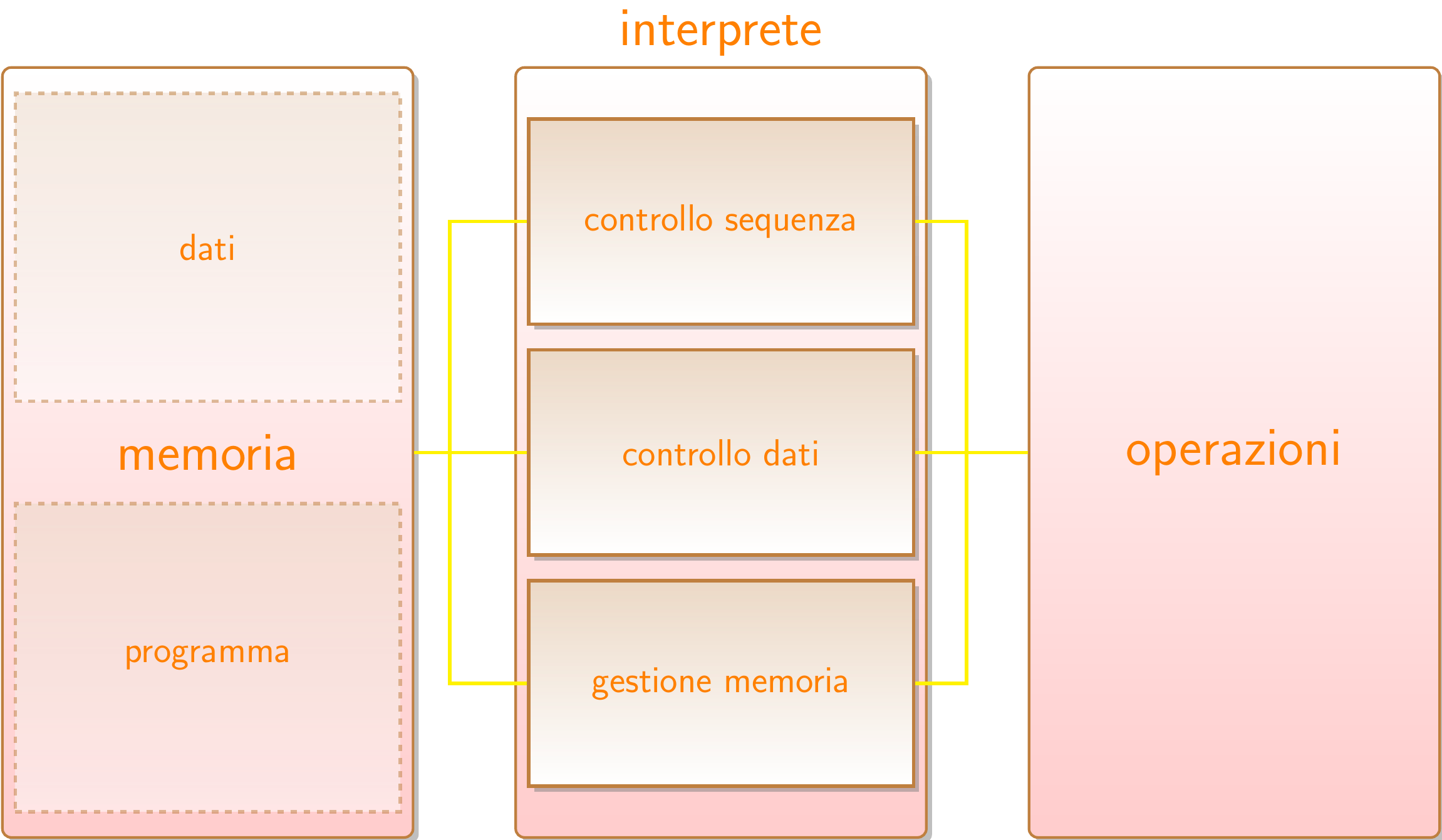
Macchine e Linguaggi
Macchina fisica (calcolatore) $\mathcal{M}$: dispositivo capace di eseguire istruzioniespresse in un linguaggio comprensibile per tale esecutore
- Linguaggio di macchina $\mathcal{L}$: linguaggio formale compreso dalla macchina
utile a descrivere algoritmi
insieme di algoritmi e strutture dati che permettono di memorizzare ed eseguire programmi in $\mathcal{L}$
Programma
Programma: descrizione di un algoritmo come sequenza di istruzioni in dato un linguaggio di programmazione $\mathcal{L}$Definisce un processo deterministico (meccanico)
La computazione di un qualunque programma in $\mathcal{L}$ può essere simulata da una MdT- dato un numero anche alto di transizioni
- non fa altro che cambiare bit in memoria
Linguaggio TM
| ␢ | $v_1$ | ␢ | $v_2$ | ␢ | $\ldots$ | ␢ | $v_k$ | ␢ | $v_{k+1}$ | ␢ | $\ldots$ | ␢ $v_n$ | ␢ | ␢ ␢ ␢ ␢ ␢ ␢ ␢ ␢ ␢ ␢$ $ |
| var. input | var. locali | * | registri e spazio di lavoro | |||||||||||
| INIT $v_i$ | inizializza la variabile locale $v_i$ a $0$ |
| HOME $t$ | sposta la testina in posizione iniziale * avendo allocato $t$ variabili |
| LOAD $v_i,t$ | carica il valore della la variabile $v_i$ nel registro $t$ |
| STOR $v_i,t$ | memorizza il valore del registro $T$ nella variabile $v_i$ |
| RETURN $v_i$ | cancella le variabili e lascia la variabile $v_i$ nella posizione di output |
| CLEAR $t$ | cancella il valore del registro $t$ |
| BRN $l,t$ | salta all'istruzione con l'etichetta $l$ se il valore del registro $t$ è $0$ |
| GOTO $l$ | salta all'istruzione etichettata con $l$ |
| NOP | nessuna operazione (spesso con GOTO) |
| INC $t$ | incrementa il valore del registro $t$ |
| DEC $t$ | incrementa il valore del registro $t$ |
| ZERO $t$ | azzera il valore del registro $t$ |
Linguaggio WHILE
\[ \begin{eqnarray} P & \to & \mathtt{begin}\ \mathtt{end} \mid \mathtt{begin}\ S\ \mathtt{end}\\ S & \to & I \mid S ; I\\ I & \to & A \mid \mathtt{while}\ T\ \mathtt{do}\ I \mid P\\ A & \to & V\ \mathtt{=}\ \mathtt{O} \mid V\ \mathtt{=}\ \mathtt{s(}V\mathtt{)} \mid V\ \mathtt{=}\ \mathtt{p(}V\mathtt{)}\\ T & \to & V \mathtt{\neq} V\\ V & \to & V \mid V L \mid V C\\ L & \to & \mathtt{A} \mid \mathtt{B} \mid \ldots\\ C & \to & \mathtt{0} \mid \mathtt{1} \mid \cdots \mid \mathtt{9} \end{eqnarray} \]Linguaggio WHILE | un programma
begin
X = 1;
Y = 1;
while Y ≠ 13 do
begin
Y = X + Y;
X = X + Y
end
R = X
end
Struttura Macchina Astratta
Ciclo d'esecuzione | Interprete dei Comandi
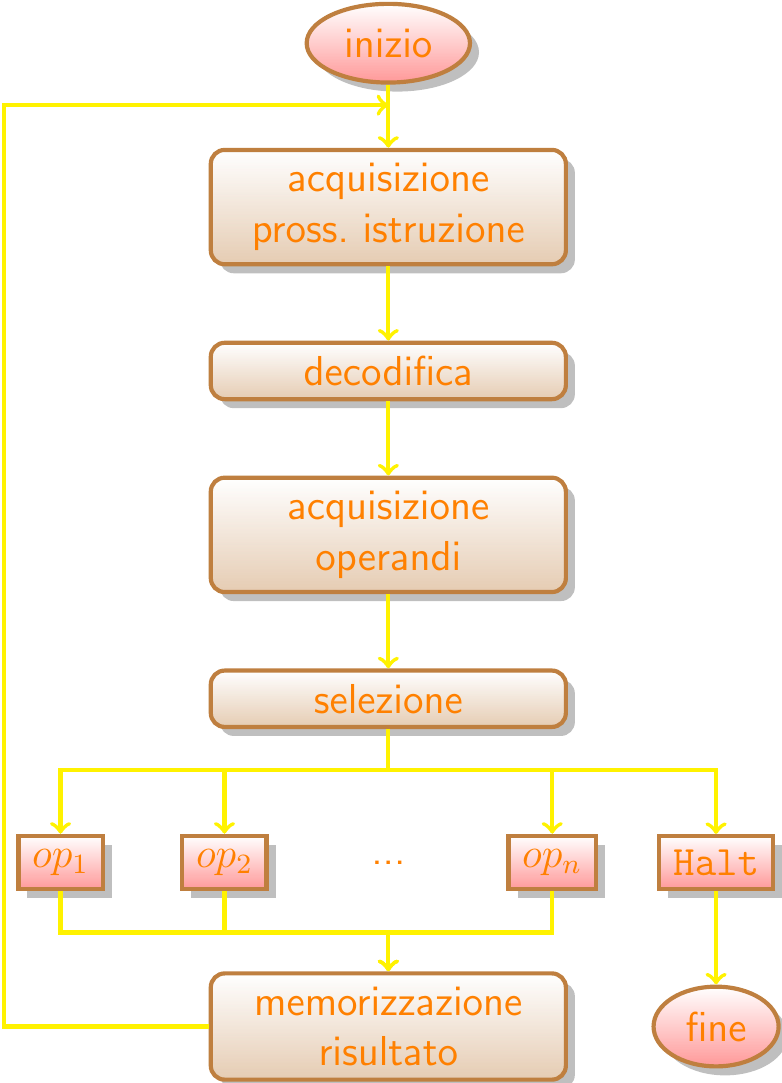
- Acquisizione da memoria della prossima istruzione
- Decodifica dell'operazione e dei suoi operandi
- Acquisizione degli operandi
- Esecuzione dell'operazione
- Memorizzazione del risultato
- Se l'istruzione è HALT
- termina
- vai al passo 1.
Traduzione | Interpretazione
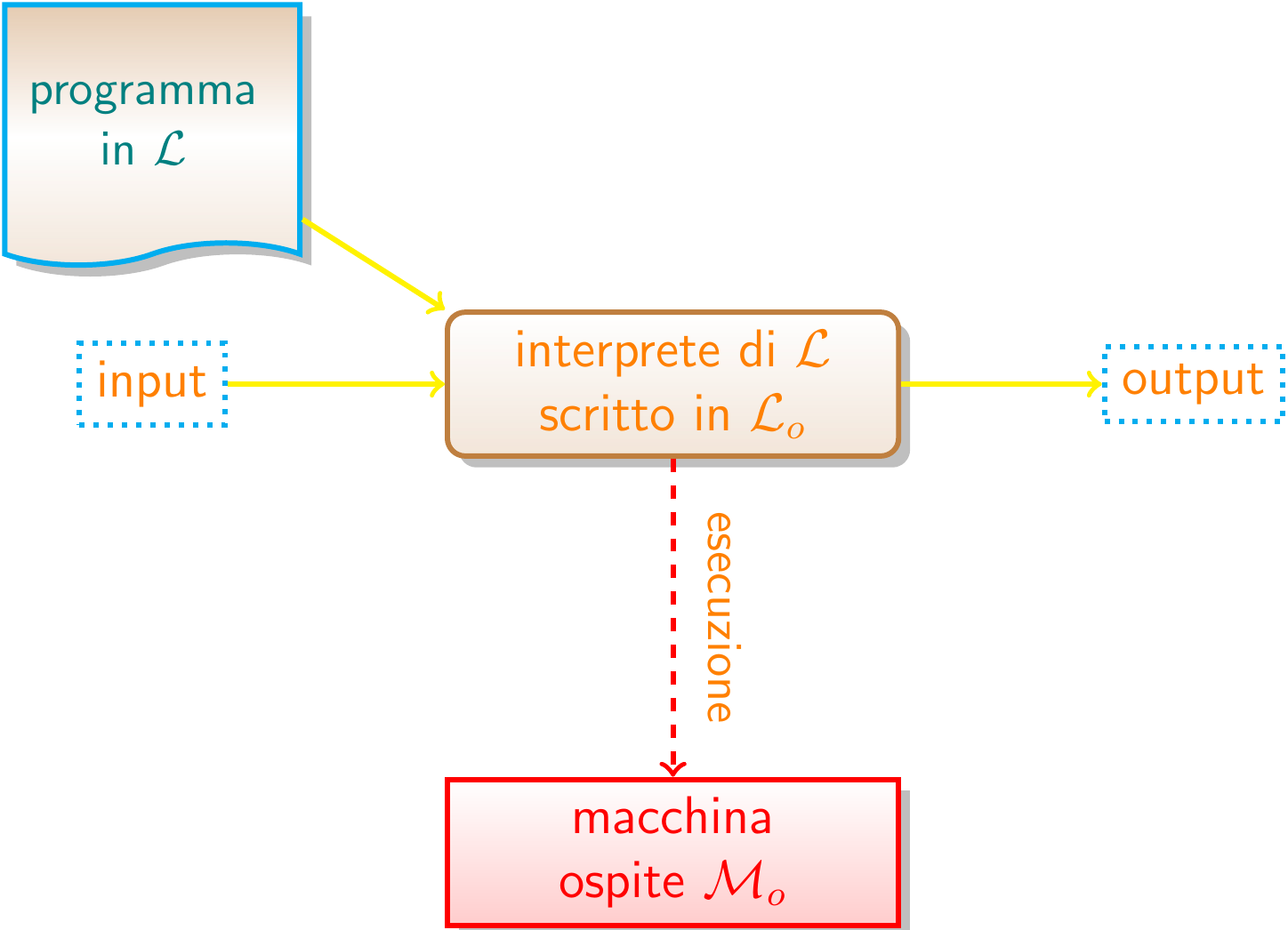
Traduzione | Compilazione
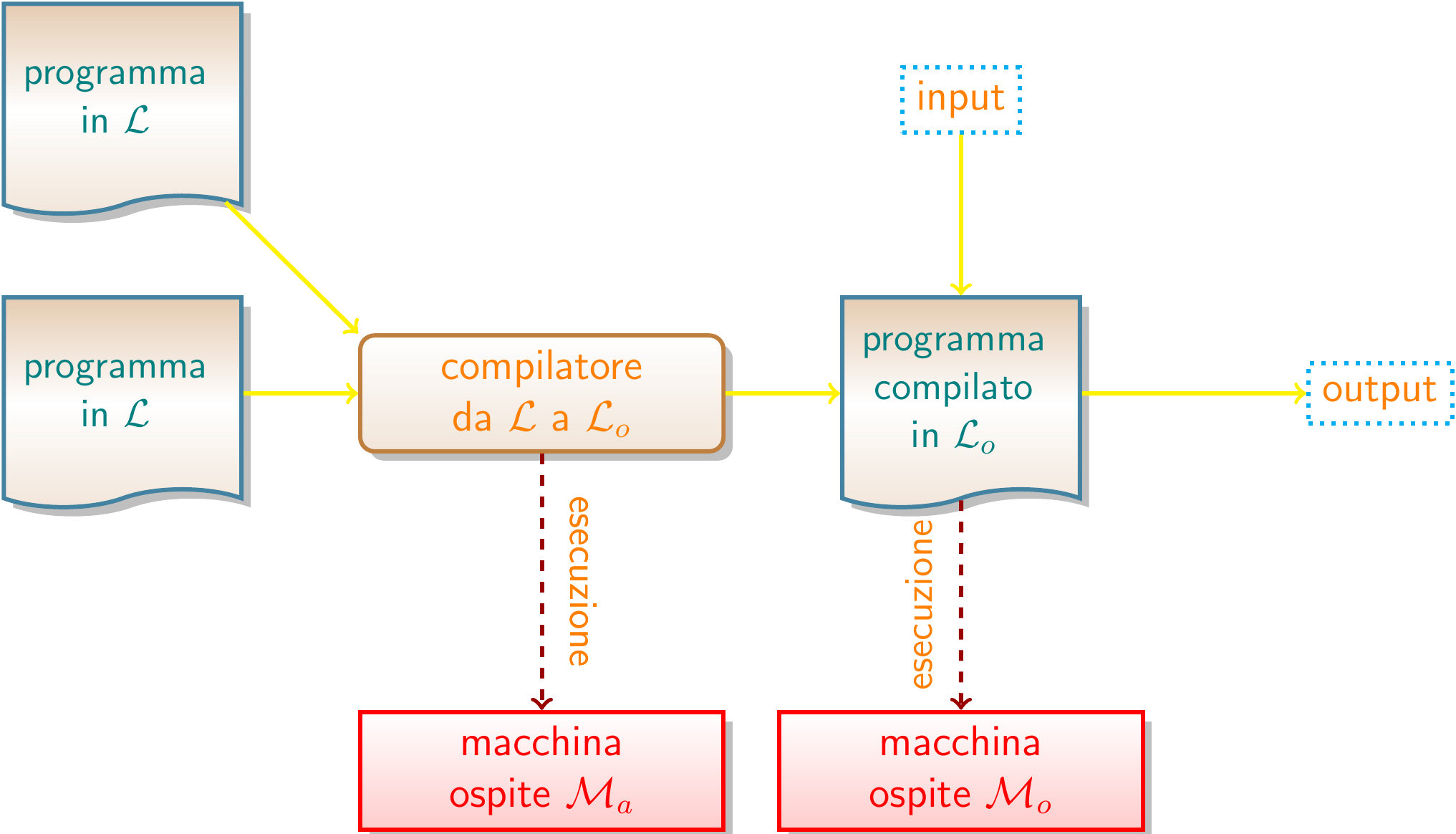
Traduzione | Ibrida
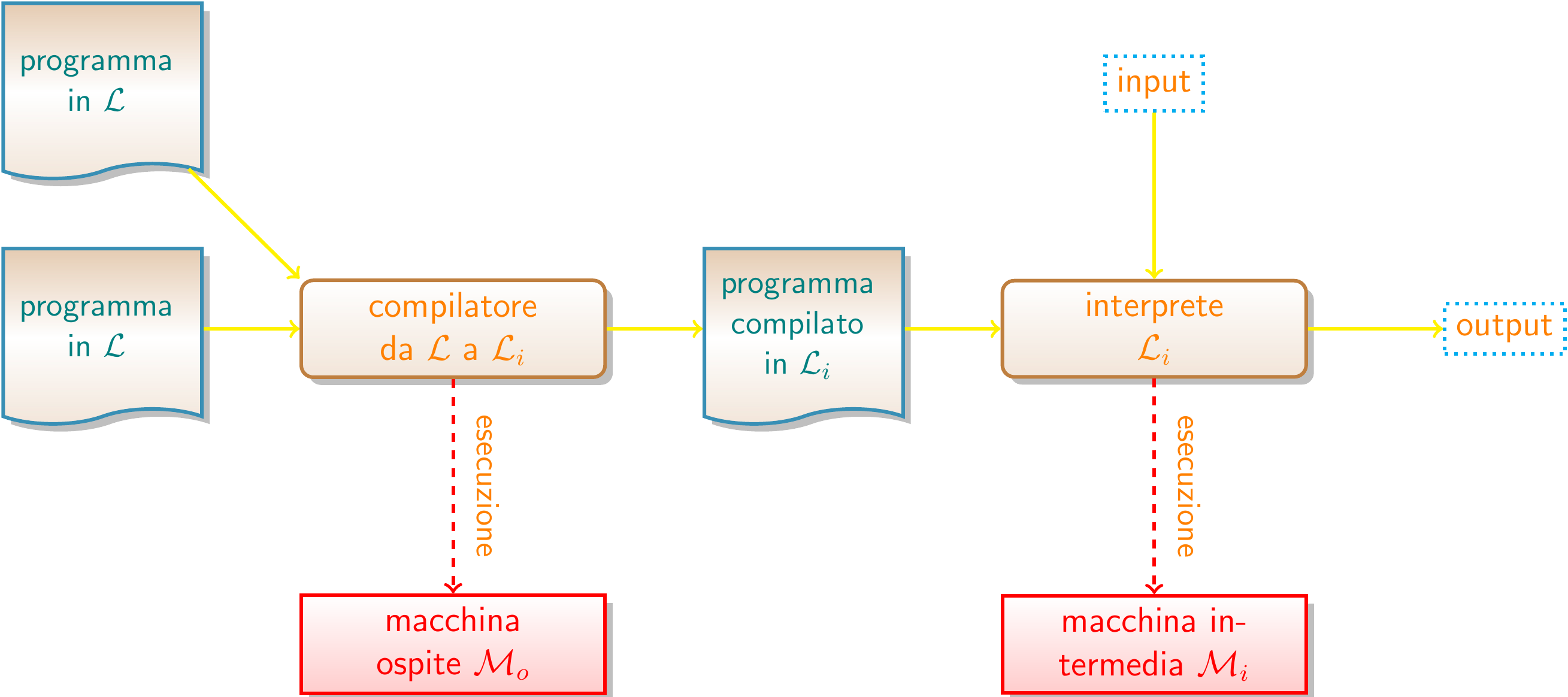
Schema Compilazione
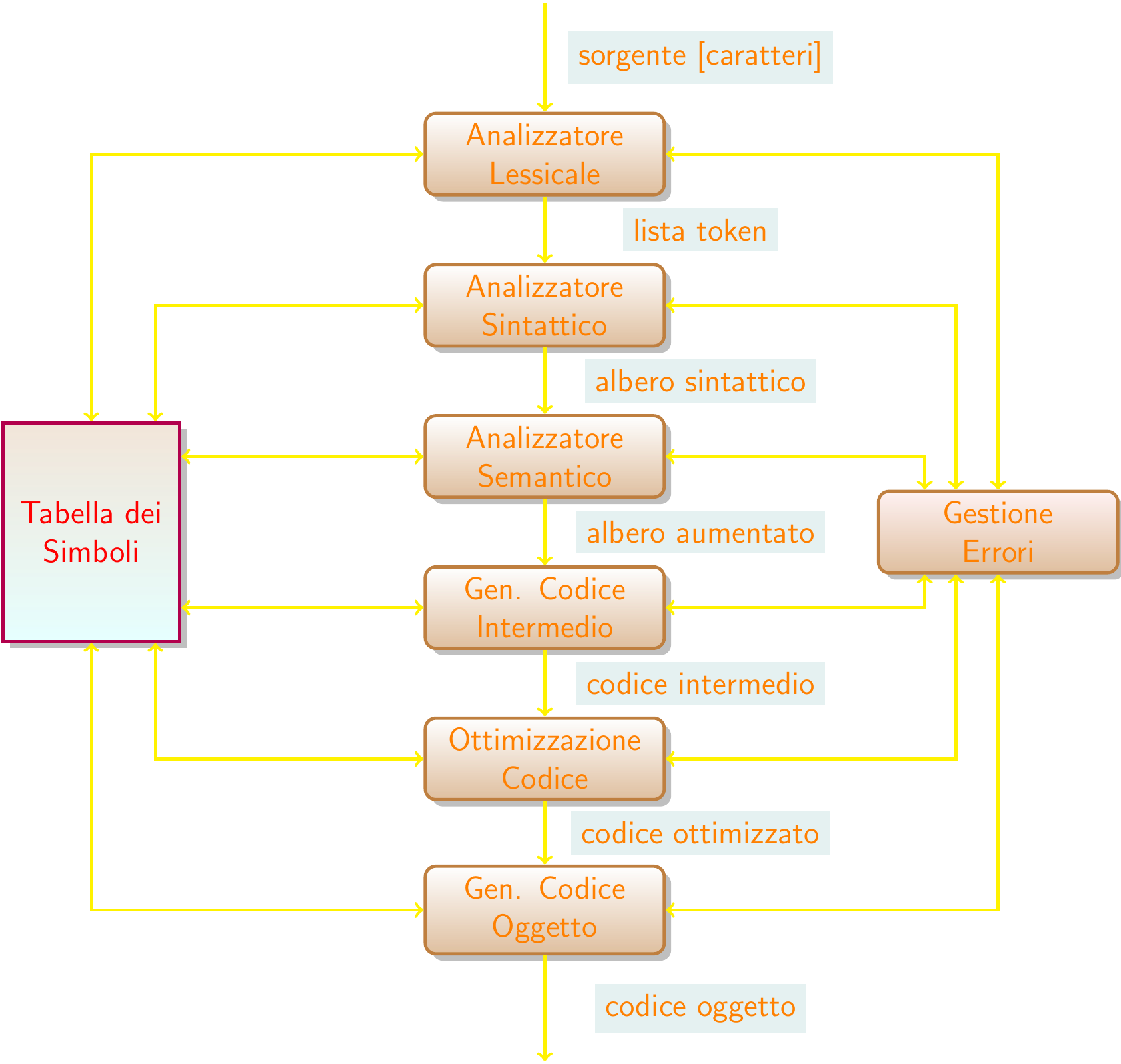
Gerarchia di Macchine Astratte

Altri Paradigmi di Programmazione
Non solo linguaggi imperativi programmi basati su sequenze di istruzioni- paradigma Logico programmi come formule logiche
sommalista([],0). sommalista([N|Resto],S) :- sommalista(Resto,SR), S is N+SR.
- paradigma Funzionale programmi come funzioni matematiche
sommalista(L) = cond(vuota(L), 0, testa(L)+sommalista(coda(L)))
FINE
Domande ?
offline www.di.uniba.it/~fanizzi
Riferimenti
Testi
- Sudkamp: Languages and Machines An Introduction to the Theory of Computer Science. Addison-Wesley
- Sebesta: Concepts of Programming Languages 12/ed. Pearson
- Toffalori et al.: Teoria della computabilità e della complessità McGraw-Hill
- Hofstadter: Gödel, Escher, Bach: un' eterna ghirlanda brillante. Adelphi
- Doxiadis e Papadimitriou: Logicomix Guanda (graphic novel)
Link
- Linguaggio Formale su Wikipedia
- Introduzione ai Linguaggi Formali su Wikiversity
- JFLAP: www.jflap.org
- Automaton Simulator: automatonsimulator.com
- Simulatore di MdT: turingmachinesimulator.com
- Automi Cellulari: Gioco della Vita

